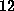next up previous contents index
Next: Elim Up: Partial Function Type Previous: Formation

Intro

  .
  H,r:ind(z,x¯.T;a) >> Gagggggggby ind r over A 
 ¯[EXT foobar]¯[EXT foobar] H >>  in  A>  B 				by intro at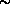 


>>  A>  B  in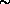 


f: A>  B , x:A >> b in 


f: A>  B , x:A, b >> b in B 

  .
  H,r:ind(z,x¯.T;a) >> Gagggggggby ind r over A 
 ¯[EXT foobar]¯[EXT foobar] H >>  =  in  A>  B 				by intro at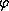 


>>  in  A>  B


>>  in  A>  B


>> {x:A | dom()(x)} = 
{x:A | dom()(x)}  in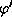 


x:{x:A | dom()(x)}
>> [x] = [x]  in B 

  .
  H,r:ind(z,x¯.T;a) >> Gagggggggby ind r over A 
 ¯[EXT foobar]¯[EXT foobar] H >> g[a] in B 				by intro using  A>  B


>> g in  A>  B


>> a in {x:A | dom(g)(x)}



  .
  H,r:ind(z,x¯.T;a) >> Gagggggggby ind r over A 
 ¯[EXT foobar]¯[EXT foobar] H >> dom(g) in A->
 				by intro using  A>  B


>> g in  A>  B


>>  A>  B  in

Richard Eaton
Thu Sep 14 08:45:18 EDT 1995