next up previous contents index
Next: Elim Up: Inductive Type Proof Previous: Formation

Intro

  .
  H,r:ind(z,x¯.T;a) >> Gagggggggby ind r over A 
 ¯[EXT foobar]¯[EXT foobar] H >>  rec(z,x.T;a)  				by intro at 
		


>> 
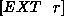
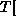
\ x.rec(z,x.T;x)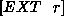
						


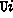
>>  rec(z,x.T;a)  in 



  .
  H,r:ind(z,x¯.T;a) >> Gagggggggby ind r over A 
 ¯[EXT foobar]¯[EXT foobar] H >> r in  rec(z,x.T;a)  				 by intro at 


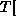
>> r in 
\ x.rec(z,x.T;x)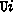


>>  rec(z,x.T;a)  in 



  .
  H,r:ind(z,x¯.T;a) >> Gagggggggby ind r over A 
 ¯[EXT foobar]¯[EXT foobar] H >> rec_ind(p; h,.g) in 


 by intro over  using y:A# rec(z,x.T;y) new 


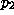
:(y:A#Z(y))->( in y:A# rec(z,x.T;y)),


h::(y:A#Z(y))->G,


:y:A#(
)
>> g in 


>> p in y:A# rec(z,x.T;y)

Richard Eaton
Thu Sep 14 08:45:18 EDT 1995