Elim

  .
  H,r:ind(z,x¯.T;a) >> Gagggggggby ind r over A 
 ¯[EXT foobar]¯[EXT foobar] H,r: rec(z,x.T;a) , >> G 				 by elim r		

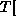
H,r:
\ x.rec(z,x.T;x)
, >> G 						 

  .
  H,r:ind(z,x¯.T;a) >> Gagggggggby ind r over A 
 ¯[EXT foobar]¯[EXT foobar] H,r: rec(z,x.T;a)  >> G<a,r>p
				rec_ind(<a,r>;)

 by elim r over y:A# rec(z,x.T;y)\
using p. new 

p:(y:A#Z(y))->(p in y:A# rec(z,x.T;y)),

h:p:(y:A#Z(y))->G,

p:y:A#(
) >> G
						

>> a in A