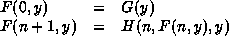Another major difference between the Lambda--prl rules and the Nuprl rules is the treatment of equality and simplification. The logic of Lambda--prl is sufficiently simple that all equality reasoning can be lumped into a single rule. Similarly, simplification of terms is handled by a single rule. The two are combined, together with some elementary arithmetic reasoning, into a decision procedure called arith which handles nearly all of the low--level details of Lambda--prl proofs. However, the additional expressiveness of the Nuprl logic prevents such a simple solution. For each term constructor there is a rule of equality, for each elimination form there is a computation rule, and there is a general rule of substitution.
For instance, the equality rule for inl is as follows.
For decide there are two equality rules: the basic equality rule for the constructor and a computation rule. The goals are, respectively,>> inl(
) = inl(
) in
|
by intro
>>
=
in

>>
in
and>> decide(
;
;
) = decide(
;
;
) in
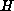
Equations obtained with these rules can be used by the equality and substitution rules.>> decide(inl(
);
;
) =
in