One creates definitions and theorems in two stages.
First, one creates a slot in the library where the new object is to
be stored by issuing the create command
followed by the name of the object,
the kind
of the object and
a place for the name ( top, bottom or before or after another
name).
The general form of the ``create''
command is
create name kind place.
An example of such a command follows.
create t1 thm topThe result is the display of
? t1
THM
as a new library entry.
The system does not recognize this as an object but rather as a place where the
object t1 will eventually reside.
The mark ? is called
a status mark. The status of an object can be any
one of the following:
.
The second stage in creating an object
involves invoking the proof and text editors on the library
object created in the first
stage described above.
One does so by asking to view the object:
view name.
Issuing view t1 results in a new window as shown in figure 
.
If an object were present, it would appear in the window;
at this stage, however, no object has been created, so one sees ? top.
Since the object being edited is a theorem,
the new window produced is a view of the proof editor, or refinement
editor;
if the object were a definition, then the system invokes the text editor.
Definitions will be discussed at greater length in the next section.
The refinement editor is a editor for tree--structured objects and is used for building
proof trees.
It is discussed in detail in chapter 4; at present it may be viewed
as the place where theorems are displayed.
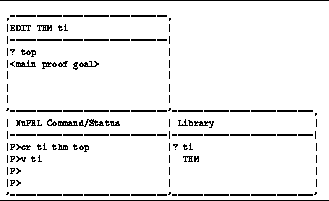
Figure: Appearance of the Screen after the Proof Editor Is Invoked
To enter a theorem statement at this stage, one invokes
the text editor (ted) by pressing the
select key, SEL
,SEL
}
or by clicking the left key on the mouse with the mouse cursor in
< main proof goal>.
This opens a new window as shown in figure .
These windows can of course be repositioned, resized or elided
(moved off to the edge of the screen) .
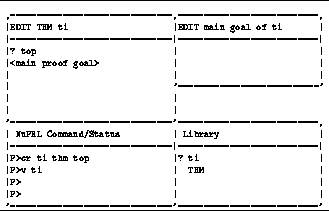
Figure: Appearance of the Screen after the Text Editor Is Invoked
One can now enter text into the text editor. As an example,
suppose one were to type >> 0=0 in int. This becomes the
statement of the theorem t1
and makes the trivial assertion that 0=0. The
>> symbol is our notation for the logical turnstile,
and
the phrase in int appears because
every statement of equality must be with
respect to some type.
One can now
leave the text editor by pressing 
;
the statement now appears in the proof--editing window.
If one were trying to prove this theorem, one would at this stage start
using the proof facilities to build the proof; this process is discussed in
detail in chapter 4.
For the present, one can simply exit from this window with 
.
The result is a new library entry for t1. The screen now looks like
figure .
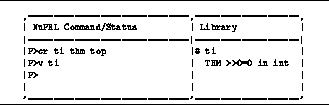
Figure: Appearance of Screen after Creating a Theorem
The status mark # indicates that this is an incomplete but syntactically correct object.