The first example of formal mathematics that we shall consider is type theory itself. Since this is the ``primitive language'' of Nuprl it will not be necessary to write definitions; the basic constructors and atomic types are already available.
As we have already mentioned, the three atomic types are
int, atom and void,
and the types are classified into a cumulative hierarchy of universes, 
,
, 
.
A type in universe 
is said to be at level i.
The atomic types all exist at level 1, i.e., in 
.
We can express this for the type of integers with the statement int in U1.
We now illustrate the mechanics of stating theorems one more time using this
theorem as an example.
Figure 
shows actual snapshots of the screen as the
theorem is produced. First, a position is created in the library using the
command cr t1 thm bot. The proof editor is entered using v t1,
and the text editor is entered by positioning the cursor on <main proof
goal> and hitting SEL
. We now type int in U1 in
the text editor
and then hit 
.
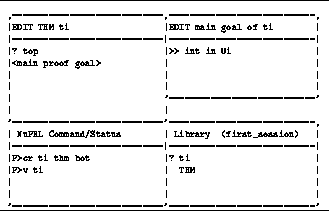
Figure: Stating a Simple Theorem